Generating territories
Contributors: Clark S. Rushing
R Skill Level: Intermediate - this activity assumes you have a working knowledge of R. If you’re not familiar with the apply family of operations in R you may wish to brush up on those before proceeding. See the help files for more information.
Objectives & Goals
Upon completion of this activity, you will:- create territories using kernel density estimates
- create territories using minimum convex polygon
- find the area of each territory
- calculate an index of density
- Extract raster data to terrtiories
Required packages
To complete the following activity you will need the following packages installed: raster sp rgeosInstalling the packages
If installing these packages for the first time consider addingdependencies=TRUE
install.packages("raster",dependencies = TRUE)install.packages("rgdal",dependencies = TRUE)install.packages("rgeos",dependencies = TRUE)install.packages("sp",dependencies = TRUE)Download R script Last modified: 2019-09-20 18:26:28
If you work with marked populations or have telemetry-like data you may be interested in constructing territories with either a minimum convex polygon or using kernel density estimation. This activity will illustrate how to go from GPS coordinates of locations for individuals to a territories using both minimum convex polygons and kernel density estimates.
We’ll use location data from a marked population of Ovenbirds breeding at Hubbard Brook Experimental Forest in New Hampshire. The data used in this activity are real data collected in 2012 - we may encounter some hic-cups along the way - we’ll sort them out as/if we encouter them.
library(raster)
library(sp)
library(ks)
Read in bird locations
The location data are stored as a csv file.
OVEN_locs <- read.csv("../Spatial_Layers/OVEN_2012_locs.csv")
## 'data.frame': 1634 obs. of 7 variables:
## $ Type : Factor w/ 1 level "WAYPOINT": 1 1 1 1 1 1 1 1 1 1 ...
## $ ident: Factor w/ 551 levels "1","10","100",..: 13 24 494 51 52 53 54 55 56 58 ...
## $ lat : num 44 44 44 44 44 ...
## $ long : num -71.7 -71.7 -71.7 -71.7 -71.7 ...
## $ Date : Factor w/ 55 levels "","1-Jun-12",..: 34 34 48 54 54 54 54 54 54 54 ...
## $ Time : Factor w/ 1566 levels "05:09:30","05:09:36",..: 826 875 112 358 360 372 399 410 428 462 ...
## $ Bird : Factor w/ 64 levels "__AO","A_KK",..: 1 1 1 1 1 1 1 1 1 1 ...
Convert points to SpatialPoints object
Now that we have the data in R we can create a SpatialPoints object.
# coords = cbind(long,lat)
# crs = WGS84
OVENpts <- sp::SpatialPoints(coords = cbind(OVEN_locs$long,OVEN_locs$lat),
proj4string = sp::CRS("+init=epsg:4326"))
# take a peek
head(OVENpts)
## class : SpatialPoints
## features : 1
## extent : -71.74627, -71.74627, 43.95437, 43.95437 (xmin, xmax, ymin, ymax)
## crs : +init=epsg:4326 +proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0
Let’s keep all the data together and make a SpatialPointsDataFrame
OVEN_spdf <- sp::SpatialPointsDataFrame(OVENpts,OVEN_locs)
head(OVEN_spdf)
## Type ident lat long Date Time Bird
## 1 WAYPOINT 11 43.95437 -71.74627 26-May-12 09:13:58 __AO
## 2 WAYPOINT 12 43.95435 -71.74624 26-May-12 09:27:42 __AO
## 3 WAYPOINT 95 43.95441 -71.74652 6-Jun-12 06:32:15 __AO
## 4 WAYPOINT 144 43.95450 -71.74707 9-Jun-12 07:23:48 __AO
## 5 WAYPOINT 145 43.95445 -71.74709 9-Jun-12 07:24:17 __AO
## 6 WAYPOINT 146 43.95437 -71.74679 9-Jun-12 07:26:39 __AO
One handy function available in R that isn’t in ArcMap (or at least it wasn’t when I stopped using it) is a function to split a shapefile based on attributes to make a series of spatial layers. The split does exactly that. We’ll use it here to make a SpatialPoints object for each individual in the dataset.
OVEN_sep <- split(x = OVEN_spdf, f = OVEN_spdf$Bird, drop = FALSE)
We now have a list, one element for each unique Bird id. We’ll use this to make our territories.
Minimum Convex Hull
Minimum convex polygon (MCP) generates a polygon that encapsulates all points for an individual. The first step is to make a minimum convex polygon for each individual. The gConvexHull does exactly that. Here we’ll using the lapply function to avoid for loops.
OVENmcp <- lapply(OVEN_sep, FUN = function(x){rgeos::gConvexHull(x)})
The above function returns a list. Ideally, we want all the polygons merged into a single SpatialPolygonsDataFrame. Before we can collapse the list we need to change the ID field in each polygon. Currently, each polygon has the same value in the ID field. Because of that - we can’t combine them. The next bit of code labels each polygon ID field as the Bird id.
OVENmcp <- mapply(OVENmcp, names(OVENmcp),
SIMPLIFY = FALSE,
FUN = function(x,y){x@polygons[[1]]@ID <- y
return(x)})
Now that the ID field is unique for each polygon we can merge the polygons together into a single SpatialPolygons object.
OVENmcp <- do.call(rbind,OVENmcp)
## class : SpatialPolygons
## features : 64
## extent : -71.756, -71.69537, 43.94234, 43.958 (xmin, xmax, ymin, ymax)
## crs : +init=epsg:4326 +proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0
Let’s finish this portion by creating a SpatialPolygonsDataFrame
OVENmcp <- SpatialPolygonsDataFrame(Sr = OVENmcp,
data = data.frame(Bird = names(OVENmcp)),
match.ID = FALSE)
## class : SpatialPolygonsDataFrame
## features : 64
## extent : -71.756, -71.69537, 43.94234, 43.958 (xmin, xmax, ymin, ymax)
## crs : +init=epsg:4326 +proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0
## variables : 1
## names : Bird
## min values : __AO
## max values : YWAY
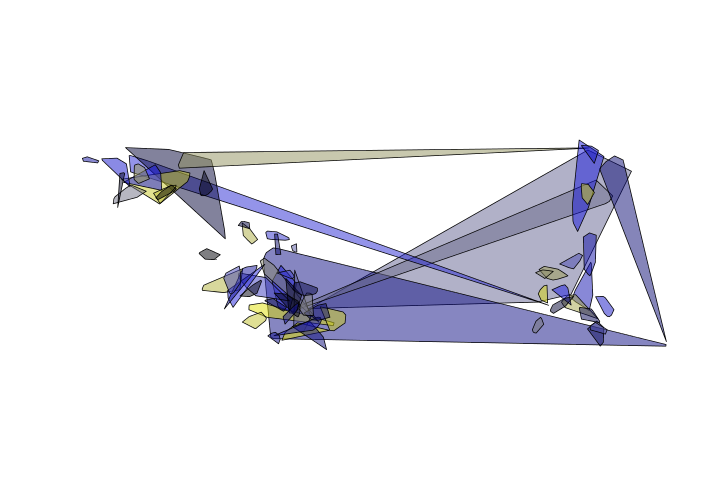
There are some issues. Looks like maybe a few points were labeled incorrectly. We’ll come back to fix those up.
Kernel density estimation
Below is just one way to estimate territories using kernel density estimates. We’ll use least-square cross validation to estimate the bandwidth - see Barg et al. 2005 for more information.
First, we’ll estimate the bandwidth for each bird. To do that we’ll use the least-squares cross validation (LSCV) estimator that is part of the ks package. We’ll use lapply again to avoid for loops. The following code will estimate the bandwidth using the coordinates for each bird. LSCV doesn’t like having duplicated points - it may return a warning. Here, we’ll just ignore those warnings for now.
bw <- lapply(OVEN_sep, FUN = function(x){ks::Hlscv(x@coords)})
## Warning in ks::Hlscv(x@coords): Data contain duplicated values: LSCV is not
## well-behaved in this case
## Warning in ks::Hlscv(x@coords): Data contain duplicated values: LSCV is not
## well-behaved in this case
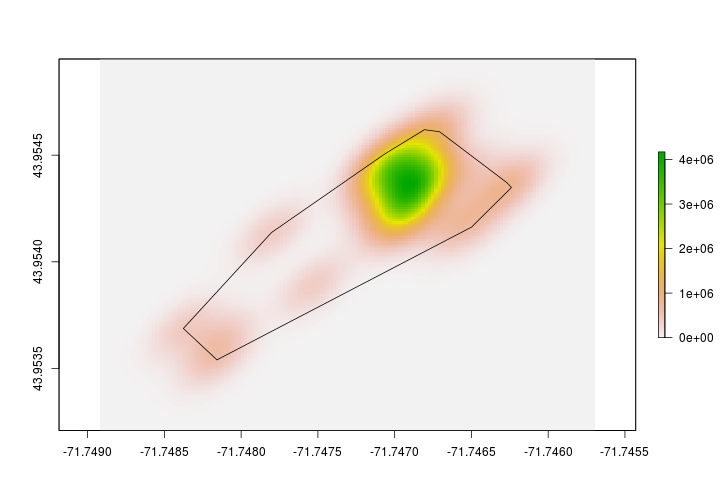
Now that we’ve estimated the bandwidth we can generate the territories. We’ll use the kde (kernel density estimate) in the ks package to create the kernel density estimate. Then in the same function call we’ll convert the kernel density estimate into a raster layer that is spatially explicit. To do this we’ll use the mapply function. See here for more information on what mapply does.
OVEN_kde <-mapply(OVEN_sep,bw,
SIMPLIFY = FALSE,
FUN = function(x,y){
raster(kde(x@coords,h=y))})
Here’s a quick peek at the difference between the MCP and KDE for the same individual.
We’re not finished yet with the making the KDE’s. Let’s create a 95% kernel density estimate. To do that we’ll first need to determine what the 95% contour value is. Then, we’ll set all raster values that are less than that value to NA. Once we have the 95% kernel density estimate, we’ll then convert the raster into a polygon so we can find the area, extract landcover data, etc.
Let’s find the 95% contour. To do this we’ll write a custom function. The function will take the kde and probability as inputs. The below function call getContour will make the 95% KDE for us.
# This code makes a custom function called getContour.
# Inputs:
# kde = kernel density estimate
# prob = probabily - default is 0.95
getContour <- function(kde, prob = 0.95){
# set all values 0 to NA
kde[kde == 0]<-NA
# create a vector of raster values
kde_values <- raster::getValues(kde)
# sort values
sortedValues <- sort(kde_values[!is.na(kde_values)],decreasing = TRUE)
# find cumulative sum up to ith location
sums <- cumsum(as.numeric(sortedValues))
# binary response is value in the probabily zone or not
p <- sum(sums <= prob * sums[length(sums)])
# Set values in raster to 1 or 0
kdeprob <- raster::setValues(kde, kde_values >= sortedValues[p])
# return new kde
return(kdeprob)
}
OVEN_95kde <- lapply(OVEN_kde,
FUN = getContour,prob = 0.95)
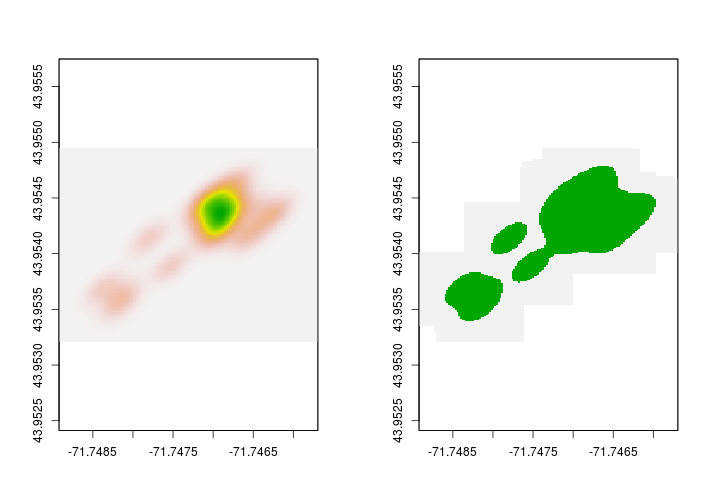
Now that we have the 95% KDE, let’s make a polygon. We’ll use raster’s rasterToPolygons to do that. First, we’ll change all the values in the 95% KDE to 1. After we do that we’ll covert to a polygon. We first convert all values to 1 so that we only make a single polygon that represents the 95% KDE.
OVEN_95poly <- lapply(OVEN_95kde,
FUN = function(x){
x[x==0]<-NA
y <- rasterToPolygons(x, dissolve = TRUE)
return(y)
})
Before we can merge the 95% KDE together into a single SpatialPolygonsDataFrame we need to change the polygon ID field. We did this above in the MCP example. We’ll use the same processes again here.
OVEN_95poly <- mapply(OVEN_95poly, names(OVEN_95poly),
SIMPLIFY = FALSE,
FUN = function(x,y){x@polygons[[1]]@ID <- y
return(x)})
Now that the ID field is unique for each polygon we can merge the polygons together into a single SpatialPolygons object.
OVEN_95poly <- do.call(rbind,OVEN_95poly)
We’ll finish this portion by adding the bird ID field to the SpatialPolygonsDataFrame. I introduce a new helper function within the sp package called getSpPolygonsIDSlots which does exactly as the function suggests - it returns the ID slot within an object of class SpatialPolygon.
OVEN_95poly$Bird <- getSpPPolygonsIDSlots(OVEN_95poly)
## Warning: use *apply and slot directly
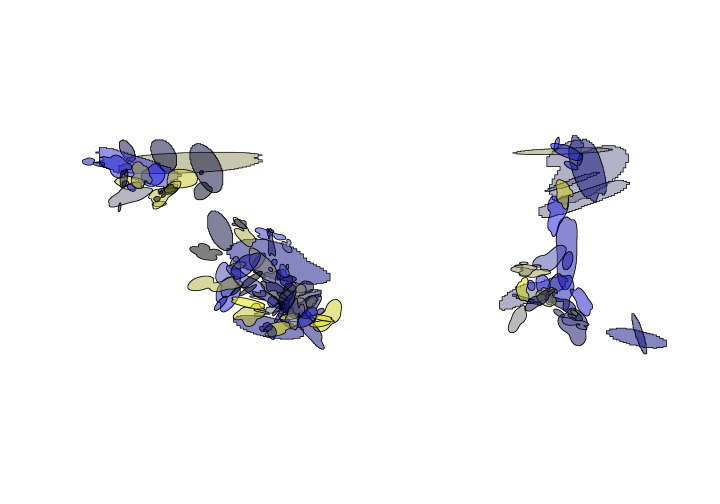
Calculate attributes / Extract raster data
Now that we have made some territories - let’s extract some information. One attribute of interest is territory size. Before we calculate the size, let’s take a look at the crs.
OVEN_95poly
## class : SpatialPolygonsDataFrame
## features : 64
## extent : -71.75641, -71.69242, 43.9414, 43.95862 (xmin, xmax, ymin, ymax)
## crs : +proj=longlat +datum=WGS84 +ellps=WGS84 +towgs84=0,0,0
## variables : 2
## names : layer, Bird
## min values : 1, __AO
## max values : 1, YWAY
Notice that the crs is WGS84 or in other words - lat/long, not projected. Let’s first project into a projection that will give us meaningful area estimates. Since these data were gathered at Hubbard Brook Experimental Forest in New Hampshire, let’s use UTM, ZONE 19 N (EPSG:32619) as our projection.
OVENkde_utm <- sp::spTransform(OVEN_95poly, sp::CRS("+init=epsg:32619"))
Now that we have projected data that is in meters we can get a more meaningful measure of area. We’ll use the gArea function in the rgeos package to calculate the area. Let’s have it return the area in hectares.
rgeos::gArea(OVENkde_utm, byid = TRUE)/10000
## __AO A_KK A_MM APRY BBAR BBAW
## 1.0673764 2.4870911 1.8667872 5.0575723 1.9110031 1.0059919
## BOGA BRAO BRAW BRGA BWAO BYAK
## 2.9517315 2.1417197 20.3285926 0.6728364 2.7020183 1.7512344
## BYWA GGAR GRAO GRAW GRGA GWAG
## 2.7786690 5.6030768 3.7193737 1.0639960 14.5445779 4.6073879
## GYAB GYAO KRAG KROA KWAG KYAR
## 35.7228287 1.1734981 1.8457727 4.1336069 0.8192061 9.5846092
## KYBA MBAY MBWA MM_A MMAY MWGA
## 6.2356445 2.1787982 2.8555932 2.5728915 3.6637620 5.0746542
## OBAK OKBA OOYA ORWA OWAK OWOA_MID
## 4.9705965 3.4475742 2.6901538 5.3687464 13.5747309 1.4972174
## OYAR PKYA PPAK PWKA PYYA RBAB
## 0.8822659 4.6840713 5.2457076 3.6238212 1.4511408 0.6944329
## RGAW RKAR ROGA RWAP RWKA RYWA
## 2.5649554 39.4765430 14.8932943 4.5950448 2.2485388 2.6918551
## WA_Y WBOA WGAY WGGA WOAW WOGA
## 4.6116720 1.5454525 21.9530011 2.9143715 1.9042253 2.3967992
## WORA WPAB WWAB WWAO YAOY YBWA
## 2.3690225 5.2167178 3.0969429 3.2959241 6.7857750 4.7502034
## YKAG YOAB YOKA YWAY
## 2.4014232 1.6383173 2.9426634 3.8435588
Let’s extract some environmental data to our territories. Here, we’ll extract elevation but the process is the same regardless of the variable so long as it’s a raster.
First, we need to read in the digital elevation model (DEM).
# read in raster
DEM <- raster::raster("../Spatial_Layers/hb10mdem.txt")
# project raster to match territories
DEMutm <- projectRaster(DEM, crs = "+init=epsg:32619")

Extract elevation values underlying the territories and append the values to the SpatialPolygonsDataFrame.
OVENkde_utm$meanElev <- extract(DEMutm,OVENkde_utm, mean)
## BirdID area_ha Elev_mean Elev_lower Elev_upper
## __AO __AO 1.067376 742.0644 727.1407 755.8415
## A_KK A_KK 2.487091 629.2352 617.2643 640.8459
## A_MM A_MM 1.866787 581.0430 557.9654 591.5341
## APRY APRY 5.057572 543.4946 523.2714 570.2570
## BBAR BBAR 1.911003 741.2363 724.1396 777.4179
## BBAW BBAW 1.005992 780.5575 732.5729 801.6216
Calculate local density metrics
We’ll just scratch the surface here but we’ll compute a basic density metric using the territories we just created. In order to do that we’ll need a raster surface of the area. We can create a basic raster layer using the raster function. Let’s set the res to something spatially meaningful. Below we set it to 100x100m or 1 hectare.
# Empty raster with 1ha resolution
study_plot_raster <- raster::raster(OVENkde_utm, res =c(100,100))
# Covert to SpatialPolygon
study_grid <- as(study_plot_raster,"SpatialPolygons")

For our simple ‘density’ metric let’s figure out how many unique birds use each one hectare grid within the system.
# Create a list with all birds wihtin each 1ha grid cell.
birds_in_ha <- sp::over(study_grid, OVENkde_utm, returnList = TRUE)
# Find how many unique birds are in each cell
study_grid$birds <- unlist(lapply(birds_in_ha,FUN=function(x){length(unique(x$Bird))}))
#convert to raster
birds.per.ha <- rasterize(study_grid,study_plot_raster,study_grid$birds)
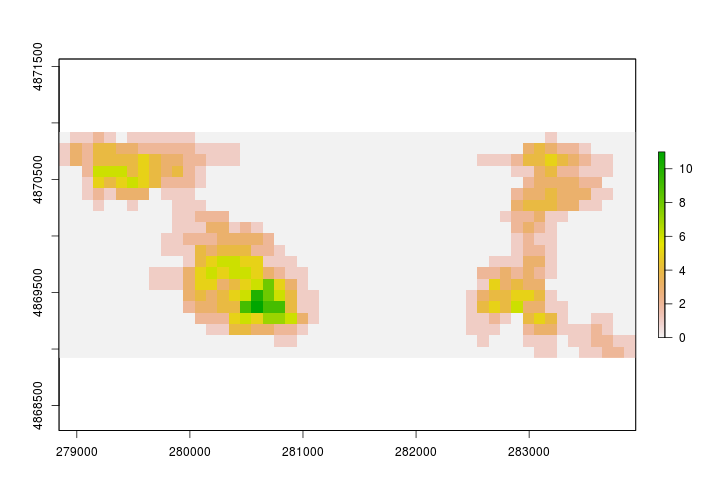
The figure above is a bit misleading. It’s unlikely that there are no Ovenbirds between our study areas.
Challenge:
Take a minute to think about how you may go about removing the areas between our study plots (where we didn't follow individuals). There is more than one way to complete this task. How could you use Spatial Predicates, extract or over to determine which 1 hectare grids were sampled. Perhaps dissolving (gUnion) may be useful.
